Les constructions impossibles

Notre cerveau cherche constamment à analyser les images visuelles en termes spatiaux, afin de nous aider à appréhender notre environnement.
C'est ainsi que, comme nous l'avons vu, de simples lignes sur une surface en deux dimensions nous suggèrent des reliefs, et des formes géométriques colorées semblent s'animer d'une vie propre.

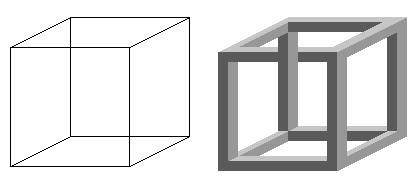
Il s'agit de regarder les cubes ci-contre pour s'en convaincre.
Le cube de verre, aussi simple soit-il, nous donne trop d'indices (effets de lumière) pour nous déstabiliser. Nous avons une impression de réalité.


Le cube dessiné de douze lignes noire ne fait qu'évoquer cette réalité et nous fait plus facilement basculer dans l'illusion d'optique. (Si ce cube était réel, laquelle de ses faces se situerait derrière? hum...)

La géométrie est à la base de ce phénomène. En effet, la géométrie euclidienne nous fait entrer dans un système logique de représentation du réel pour mieux nous confondre.

Observons maintenant ce cube simple (nommé cube de Necker) et une illusion d'optique basé sur cette ambiguïté.

Le cube de droite imite les effets de lumière du monde réel, mais sa construction ne respecte pas les lois de la perspective. C'est ce qu'on appelle une construction impossible.

Impossible, parce que ces figures n'existent qu'au niveau graphique, en deux dimensions. On ne pourrait construire un objet en trois dimensions selon les mêmes règles.
Certains artistes ont essayé, mais leur oeuvre (comme le cube de bois ci-contre) ne reproduit l'illusion que si on le regarde que d'un seul point de vue (comme dans le cas des anamorphoses, qui ne sont que le produit de la déformation d'une image). La photographie ci-contre ne fait alors figure que d'habile trucage.


Le dessin en deux dimension est si puissant par sa force de suggestion que, comme dans le cas du carré ci-contre, on a parfois pas besoin de dessiner une ligne pour la faire apparaître.


Ce qui nous fascine en réalité, c'est le côté ambigu de ces illusions d'optique, qui semblent nous proposer une vision spatiale, sans jamais nous permettre de la vérifier par l'expérience. Nous savons que ces dessins ne sont que des traits sur du papier, mais pourtant, nous voyons bel et bien un effet de profondeur et nous en ressentons un vertige.


Dans le cas des constructions impossibles, cela va encore plus loin: on nous fait croire à construction tout en nous révélant son impossibilité.


L'une des construction impossible les plus connues est sans doute le Blivet, aussi appelé « trident à deux dents », « fourche du diable » et « la chose à trois jambes ». La force de cette illusion est due au fait que notre regard se perd dans la linéarité de la forme. Ce n'est qu'un dessin, mais nous ne pouvons nous empêcher d'y voir la représentation d'un objet en 3D. 

Souvent utilisée en illustration, cette forme reste convaincante même lorsqu'on y ajoute des jeux d'ombres et de lumières.

C'est ainsi que certains artistes ont basé leur oeuvre entière sur l'ambiguïté que permettent le dessin géométrique.


Le néerlandais M.C. Escher est sans doute le plus connu d'entre eux. Féru de mathématiques, il a poussé potentiel des illusions d'optiques jusqu'à ses limites, produisant des oeuvres qui allient la sobriété de la géométrie avec l'expressivité du dessin. Voici, pour terminer ce bref aperçu de l'univers des constructions impossibles, certaines de ces réalisations.

Les illusions d'optiques, suite: les anamorphoses.